Esteganografía para programadores Python

Contenido

1. Compresión y descompresión en JPEG
2. Acceso a los coeficientes DCT
3. Incrustación en coeficientes DCT
   1. Introducción
   2. LSB matching
   3. matrix-embedding
4. Wet Paper Codes
5. Incrustación adaptativa
6. Compresión en plataformas
   

Compresión y descompresión en JPEG

El formato JPEG (Joint Photographic Experts Group) es un estándar ampliamente utilizado para la compresión de imágenes digitales. Fue desarrollado en 1992 por el comité del mismo nombre con el objetivo de reducir el tamaño de los archivos de imagen manteniendo una calidad visual aceptable. A diferencia de otros formatos como PNG o BMP, JPEG emplea un esquema de compresión con pérdida, lo que significa que se elimina parte de la información visual menos perceptible para el ojo humano con el fin de alcanzar mayores tasas de compresión. Esta técnica permite reducir significativamente el tamaño del archivo, lo que hace que JPEG sea especialmente útil para almacenamiento, transmisión en la web y aplicaciones multimedia.

Una de las principales características del formato JPEG es su capacidad de controlar el nivel de compresión, lo que permite ajustar el equilibrio entre calidad y tamaño del archivo. También es compatible con diferentes espacios de color, como RGB y YCbCr, y emplea técnicas como el submuestreo de crominancia para optimizar la compresión. Sin embargo, cuando se aplica una compresión elevada, pueden aparecer artefactos visuales, como el efecto de bloques o la pérdida de detalles en texturas finas.

Gracias a su eficiencia y compatibilidad, el formato JPEG se ha convertido en el estándar predominante para el almacenamiento y distribución de imágenes. Es ampliamente utilizado en cámaras digitales, teléfonos móviles y plataformas en línea, donde la reducción del tamaño de los archivos es crucial para optimizar el almacenamiento y la velocidad de transmisión. Además, el algoritmo de compresión JPEG ha influido en otros estándares de codificación de imagen y video, como el formato MPEG.

El primer paso en la compresión JPEG consiste en transformar la imagen desde el espacio de color RGB al espacio de color YCbCr. Esta conversión se realiza porque el modelo RGB, aunque adecuado para la visualización en pantallas, no es eficiente para la compresión de imágenes. En cambio, el espacio YCbCr separa la información de luminancia de la información de color, lo que permite aplicar técnicas de compresión que reducen el tamaño del archivo sin afectar significativamente la percepción visual.

En el espacio YCbCr, el canal Y representa la luminancia o brillo de la imagen, mientras que los canales Cb y Cr contienen la información de crominancia, es decir, la diferencia entre el color azul y el color rojo respecto a la luminancia. La conversión de RGB a YCbCr se realiza mediante una combinación lineal de los valores de los canales de color originales. Las ecuaciones utilizadas en la conversión estándar son las siguientes:

\(Y = 0.299 R + 0.587 G + 0.114 B\) \(Cb = 128 -0.1687 R - 0.3313 G + 0.5 B\) \(Cr = 128 + 0.5 R - 0.4187 G - 0.0813 B\)

El canal de luminancia Y es el más importante para la percepción del detalle en la imagen, ya que el ojo humano es más sensible a los cambios de brillo que a los cambios de color. Esto permite aprovechar la conversión al espacio YCbCr para aplicar técnicas de submuestreo en los canales de crominancia sin que la pérdida de información sea fácilmente perceptible.

Una vez que la imagen ha sido convertida al espacio de color YCbCr, el siguiente paso en la compresión JPEG es el submuestreo de crominancia. Este proceso reduce la cantidad de información en los canales de color Cb y Cr sin afectar significativamente la percepción visual. Dado que el ojo humano es mucho más sensible a los cambios de luminancia que a los cambios de color, es posible disminuir la resolución de los componentes cromáticos sin que la imagen resultante se vea afectada de manera notable.

El submuestreo de crominancia se basa en la agrupación de píxeles adyacentes para compartir información de color. Dependiendo de cuánta información se conserve en los canales Cb y Cr en comparación con el canal de luminancia Y, se pueden emplear distintos esquemas de submuestreo. En el esquema 4:4:4, no se realiza reducción, por lo que cada píxel mantiene su información de color completa. En el esquema 4:2:2, la resolución de los componentes cromáticos se reduce a la mitad en la dirección horizontal, lo que implica que cada dos píxeles comparten la misma información de color. Por otro lado, en el esquema 4:2:0, la crominancia se reduce tanto en la dirección horizontal como en la vertical, haciendo que cada bloque de cuatro píxeles comparta un único valor de Cb y Cr. Este último esquema es el más utilizado en la compresión JPEG debido a su eficiencia en la reducción de datos sin una pérdida perceptible de calidad.

Desde un punto de vista matemático, el submuestreo de crominancia puede entenderse como un proceso de promediado o eliminación de ciertos valores en la matriz de crominancia, dependiendo del esquema seleccionado. En el caso del submuestreo 4:2:0, la matriz de valores Cb y Cr se reduce a la mitad en ambas dimensiones, almacenando solo una cuarta parte de la información original de color. A pesar de esta reducción, cuando la imagen es reconstruida durante la descompresión, la interpolación de los valores de crominancia permite recuperar una representación visualmente coherente de los colores.

El submuestreo de crominancia es un paso esencial en la compresión JPEG, ya que permite reducir significativamente la cantidad de datos sin afectar de manera notable la calidad percibida de la imagen. Combinado con la transformada discreta del coseno y la cuantización, este proceso contribuye a obtener archivos de imagen altamente comprimidos con una degradación mínima en su apariencia visual.

Después del submuestreo de crominancia, el siguiente paso en la compresión JPEG es la división de la imagen en bloques de 8x8 píxeles. Este proceso es fundamental porque permite aplicar la transformada discreta del coseno de manera eficiente en cada bloque, lo que facilita la compresión de los datos.

La elección de bloques de 8x8 se debe a un compromiso entre eficiencia computacional y calidad de compresión. Cada bloque de 8x8 se procesa de manera independiente. Esto significa que los píxeles dentro de un bloque influyen solo en la compresión de ese bloque en particular, sin afectar a los bloques vecinos. Esta independencia entre bloques tiene un efecto importante en la calidad de la imagen comprimida, ya que en niveles altos de compresión pueden aparecer artefactos en forma de discontinuidades visibles entre bloques, conocidos como efecto de bloque.

Una vez dividida la imagen en estos bloques, cada uno de ellos se somete a la transformada discreta del coseno, que permite representar la información espacial del bloque en términos de frecuencias. Este paso es esencial para la compresión, ya que facilita la eliminación de información redundante y la reducción del tamaño del archivo sin una pérdida significativa de calidad visual.

Una vez aplicada la transformada discreta del coseno a cada bloque de 8x8 píxeles, se obtiene una representación en términos de frecuencias espaciales. En esta nueva representación, los coeficientes de menor frecuencia corresponden a las variaciones más importantes de la imagen, mientras que los de mayor frecuencia representan detalles más sutiles. Dado que el ojo humano es menos sensible a las altas frecuencias, se puede reducir la precisión de estos coeficientes sin afectar significativamente la calidad percibida de la imagen. Este proceso se conoce como cuantización y es el paso en el que se produce la mayor reducción de datos dentro del esquema de compresión JPEG.

La cuantización se lleva a cabo dividiendo cada coeficiente DCT por un valor predefinido y redondeando el resultado. Para esto, se utilizan matrices de cuantización que asignan diferentes niveles de precisión a cada coeficiente según su posición en el bloque. Los valores de estas matrices están diseñados para eliminar la mayor cantidad posible de información en las frecuencias altas, donde la pérdida de datos es menos perceptible. La cuantización puede expresarse matemáticamente como:

donde $Q(u, v)$ es el coeficiente cuantizado, $D(u, v)$ es el coeficiente DCT original y $T(u, v)$ es el valor correspondiente en la matriz de cuantización.

JPEG utiliza dos matrices de cuantización estándar, una para imágenes de luminancia y otra para imágenes de crominancia. Estas matrices pueden ajustarse para modificar el nivel de compresión, permitiendo un equilibrio entre calidad y tamaño del archivo. Un mayor nivel de compresión implica valores de cuantización más altos, lo que produce una mayor pérdida de detalle en la imagen pero también reduce significativamente el tamaño del archivo resultante.

El efecto de la cuantización se hace visible en imágenes con una compresión elevada, donde pueden aparecer artefactos como bloques evidentes y pérdida de texturas finas. A pesar de esto, la cuantización sigue siendo un paso esencial en la compresión JPEG, ya que permite una reducción drástica en la cantidad de datos a almacenar y transmitir sin una degradación excesiva en la percepción visual de la imagen.

Tras la cuantización de los coeficientes DCT, el siguiente paso en la compresión JPEG es organizar y codificar estos coeficientes para reducir aún más el tamaño del archivo. Aunque este proceso es esencial para la compresión eficiente de la imagen, desde el punto de vista de la esteganografía resulta menos relevante, ya que la manipulación de la imagen para ocultar información suele ocurrir en etapas anteriores.

El primer paso en esta fase es la conversión de los coeficientes en un vector unidimensional mediante un recorrido en zigzag. Este método ordena los coeficientes de menor a mayor frecuencia, permitiendo agrupar los valores más significativos al principio del vector y los coeficientes menos relevantes, que tienden a ser ceros después de la cuantización, al final. Esta disposición facilita la posterior compresión de los datos, ya que las secuencias largas de ceros pueden representarse de manera más eficiente.

Una vez reordenados los coeficientes, se aplica la compresión por entropía, que consiste en la codificación de los datos de manera que los valores más frecuentes utilicen menos bits. Para ello, se emplea la codificación de longitud de corrida, que compacta secuencias de ceros, seguida de la codificación de Huffman, que asigna códigos más cortos a los valores que aparecen con mayor frecuencia. Este proceso permite reducir significativamente la cantidad de información almacenada sin afectar la reconstrucción de la imagen.

El archivo JPEG final se genera combinando los datos codificados con la información necesaria para su decodificación. Esto incluye las tablas de cuantización utilizadas, las tablas de Huffman generadas y los metadatos de la imagen. Este formato estandarizado garantiza que cualquier software compatible con JPEG pueda leer y reconstruir la imagen correctamente.

Aunque esta etapa es fundamental para la compresión de la imagen, su relevancia en la esteganografía es limitada. La mayoría de las técnicas de ocultamiento de información se centran en la manipulación de los coeficientes DCT o en la alteración directa de los píxeles, por lo que la codificación por entropía y la generación del archivo tienen un impacto menor en este contexto. En los métodos de esteganografía aplicados a imágenes JPEG ya comprimidas, la inserción de información suele realizarse en fases anteriores del proceso, garantizando que los datos ocultos no se vean afectados por la codificación final.

Acceso a los coeficientes DCT

Para acceder a los coeficientes DCT de una imagen JPEG, se puede utilizar la librería python-jpeg-toolbox. A continuación, se muestra cómo cargar una imagen, extraer sus coeficientes DCT y modificarlos.

El siguiente código carga un archivo JPEG y accede a sus coeficientes DCT:

import jpeg_toolbox as jt
import numpy as np
jpeg = jt.load("image.jpeg")
dct_Y = np.array(jpeg['coef_arrays'][0])
dct_Cb = np.array(jpeg['coef_arrays'][1])
dct_Cr = np.array(jpeg['coef_arrays'][2])

Si imprimimos el contenido de los arrays podemos ver los coeficientes DCT:

>>> dct_Y.shape
(512, 512)
>>> dct_Y[:8,:8]
array([[87.,  2.,  2.,  0.,  0.,  0., -1.,  1.],
       [ 4.,  0.,  0., -2.,  1.,  0.,  0.,  0.],
       [-3.,  0., -1.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]])

Los coeficientes DCT están organizados en tres matrices, correspondientes a los canales Y, Cb y Cr. Para modificarlos, se pueden realizar cambios en estos valores y luego guardar la imagen de nuevo en formato JPEG. En el siguiente código, se modifica un coeficiente en el canal de luminancia:

dct_Y[1, 1] = 3
jpeg['coef_arrays'][0] = dct_Y
jt.save(jpeg, "image_stego.jpg")

>>> dct_Y[:8,:8]
array([[87.,  2.,  2.,  0.,  0.,  0., -1.,  1.],
       [ 4.,  3.,  0., -2.,  1.,  0.,  0.,  0.],
       [-3.,  0., -1.,  0.,  0.,  0.,  0.,  0.],
       [ 1.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.]])

Además de los coeficientes DCT, la librería permite acceder a las matrices de cuantización, que determinan el nivel de compresión de la imagen. Se pueden obtener de la siguiente manera:

>>> jpeg['quant_tables']
array([[[ 3,  2,  2,  3,  4,  6,  8, 10],
        [ 2,  2,  2,  3,  4,  9, 10,  9],
        [ 2,  2,  3,  4,  6,  9, 11,  9],
        [ 2,  3,  4,  5,  8, 14, 13, 10],
        [ 3,  4,  6,  9, 11, 17, 16, 12],
        [ 4,  6,  9, 10, 13, 17, 18, 15],
        [ 8, 10, 12, 14, 16, 19, 19, 16],
        [12, 15, 15, 16, 18, 16, 16, 16]],

       [[ 3,  3,  4,  8, 16, 16, 16, 16],
        [ 3,  3,  4, 11, 16, 16, 16, 16],
        [ 4,  4,  9, 16, 16, 16, 16, 16],
        [ 8, 11, 16, 16, 16, 16, 16, 16],
        [16, 16, 16, 16, 16, 16, 16, 16],
        [16, 16, 16, 16, 16, 16, 16, 16],
        [16, 16, 16, 16, 16, 16, 16, 16],
        [16, 16, 16, 16, 16, 16, 16, 16]]], dtype=int32)

Esto permite analizar la compresión utilizada en la imagen. Además, son necesarias si se quiere implementar la descompresión directamente en Python.

Incrustación en coeficientes DCT

Introducción

Cuando se modifica un coeficiente DCT en el dominio de la frecuencia, su efecto en la imagen se manifiesta en el dominio espacial al aplicar la transformada inversa. Dado que los coeficientes DCT representan la contribución de diferentes frecuencias a la imagen, alterar sus valores puede generar cambios en la imagen reconstruida, cuya magnitud y visibilidad dependerán del coeficiente modificado.

Cada bloque de $8 \times 8$ píxeles en la imagen se descompone en una combinación de frecuencias espaciales mediante la transformada discreta del coseno. En esta representación, los coeficientes situados en la esquina superior izquierda del bloque corresponden a las frecuencias más bajas, mientras que los ubicados en la parte inferior derecha representan las frecuencias más altas. Los coeficientes de baja frecuencia contienen la mayor parte de la información visual del bloque, mientras que los de alta frecuencia representan detalles más finos y variaciones abruptas.

Modificar los coeficientes de baja frecuencia provoca cambios globales en la apariencia del bloque de imagen correspondiente. En particular, el coeficiente DC (ubicado en la posición $(0,0)$) representa la media del bloque y su alteración afecta la luminancia general, es decir, lo hace más claro o más oscuro sin modificar sus detalles internos. En cambio, los coeficientes de alta frecuencia describen los detalles más pequeños y las transiciones abruptas en la imagen. Si se modifican estos coeficientes, pueden introducirse artefactos visuales, como patrones ondulados o ruido, que pueden hacer que la modificación sea perceptible.

Además del impacto en la estructura del bloque, la cuantización utilizada en la compresión JPEG también influye en el efecto de las modificaciones. La cuantización reduce la precisión de los coeficientes DCT, especialmente en las frecuencias más altas, eliminando detalles considerados poco relevantes para la percepción humana. Como resultado, las modificaciones en los coeficientes de alta frecuencia pueden ser atenuadas o incluso eliminadas por este proceso.

Cuando se trabaja con los coeficientes DCT de una imagen JPEG, es importante considerar el impacto que tiene la modificación de aquellos cuyo valor es cero. Estos coeficientes aparecen tras la cuantización, un proceso que reduce la precisión de los valores de frecuencia más altas en la transformada discreta del coseno. Como resultado, muchos coeficientes de alta frecuencia se redondean a cero, lo que permite una compresión más eficiente del archivo.

Desde el punto de vista visual, los coeficientes DCT de valor cero suelen corresponder a detalles de alta frecuencia, como transiciones abruptas o texturas finas. Cualquier modificación en estos valores podría introducir variaciones perceptibles en la imagen, generando patrones no naturales o ruido visual. Este efecto puede hacer que las alteraciones sean más detectables tanto para el ojo humano como para métodos de estegoanálisis.

En ciertos escenarios, la modificación de coeficientes cero podría justificarse si se diseña un esquema de inserción de información que tome en cuenta las consecuencias. Sin embargo, en la mayoría de los casos, se prefiere modificar coeficientes distintos de cero, ya que su impacto en la detectabilidad del sistema es menor.

El histograma de los coeficientes DCT de una imagen JPEG presenta una distribución característica que refleja la naturaleza de la compresión aplicada en el dominio de la transformada discreta del coseno. En términos generales, este histograma tiende a ser simétrico con respecto al eje vertical en torno al valor cero, ya que los coeficientes DCT de una imagen representan variaciones de intensidad, y estas pueden darse tanto en valores positivos como negativos con la misma probabilidad.

Esta simetría es resultado de la estructura matemática de la transformada DCT y de la distribución natural de frecuencias en las imágenes. En la mayoría de los casos, los coeficientes con valores más altos en términos absolutos son menos frecuentes, mientras que los valores cercanos a cero son mucho más comunes, debido a que la mayor parte de la energía de la imagen se concentra en los coeficientes de baja frecuencia. La cuantización acentúa esta distribución al reducir la precisión de los coeficientes de alta frecuencia y eliminar muchos de ellos al redondearlos a cero, reforzando aún más la forma simétrica del histograma.

Cuando se modifican los coeficientes DCT, la simetría del histograma puede verse alterada dependiendo del tipo de modificación aplicada. Por ejemplo, si se aplica un método de esteganografía que incrementa o decrementa ciertos coeficientes de manera sistemática sin considerar la distribución original, pueden generarse sesgos en el histograma, haciendo que una parte del espectro de frecuencias tenga mayor predominancia que su contraparte negativa. Esto puede introducir anomalías detectables mediante técnicas de estegoanálisis basadas en el análisis estadístico de los coeficientes DCT.

En la figura 1 se puede observar la simetría que se produce en el histograma DCT en una imagen JPEG de ejemplo. En el histograma completo de la figura 1a podemos ver que la barra que representa el número de coeficientes de valor 0 es extremadamente alta. En el histograma ampliado de la figura 1b podemos ver de manera más clara la simetría que se produce entre ambos lados del histograma: la barra que representa el número de coeficientes con valor $1$ tiene una altura similar a la de coeficientes con valor $-1$, la que representa coeficientes con valor $2$ tiene una altura similar a la de coeficientes con valor $-2$, etc.

(a). Histograma completo

(b). Histograma ampliado

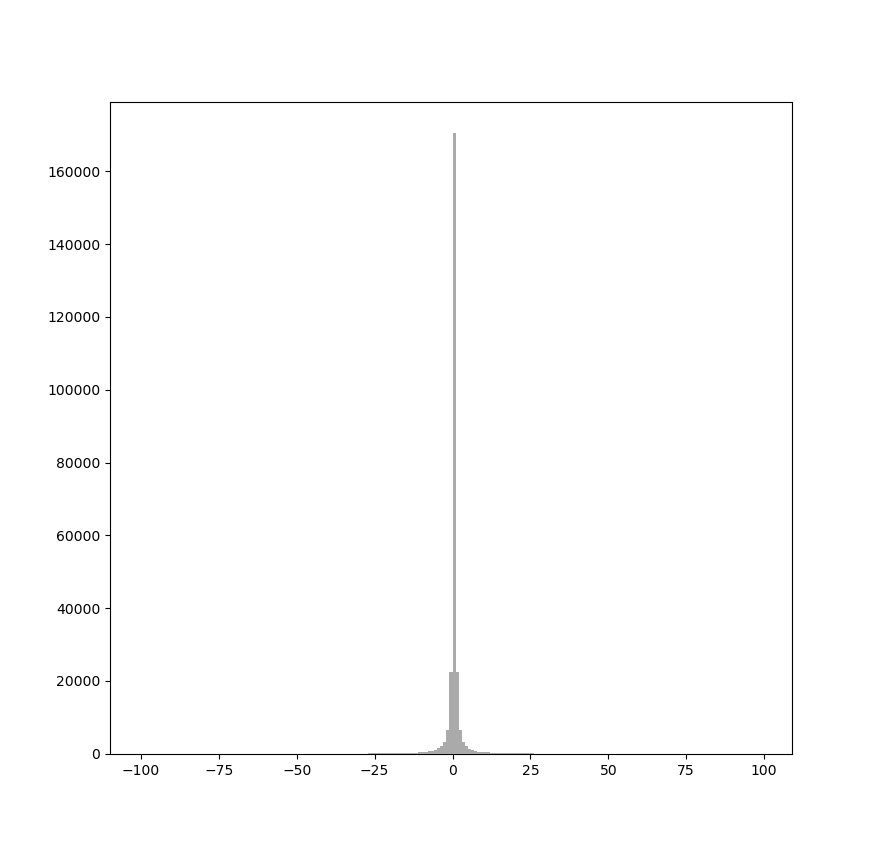
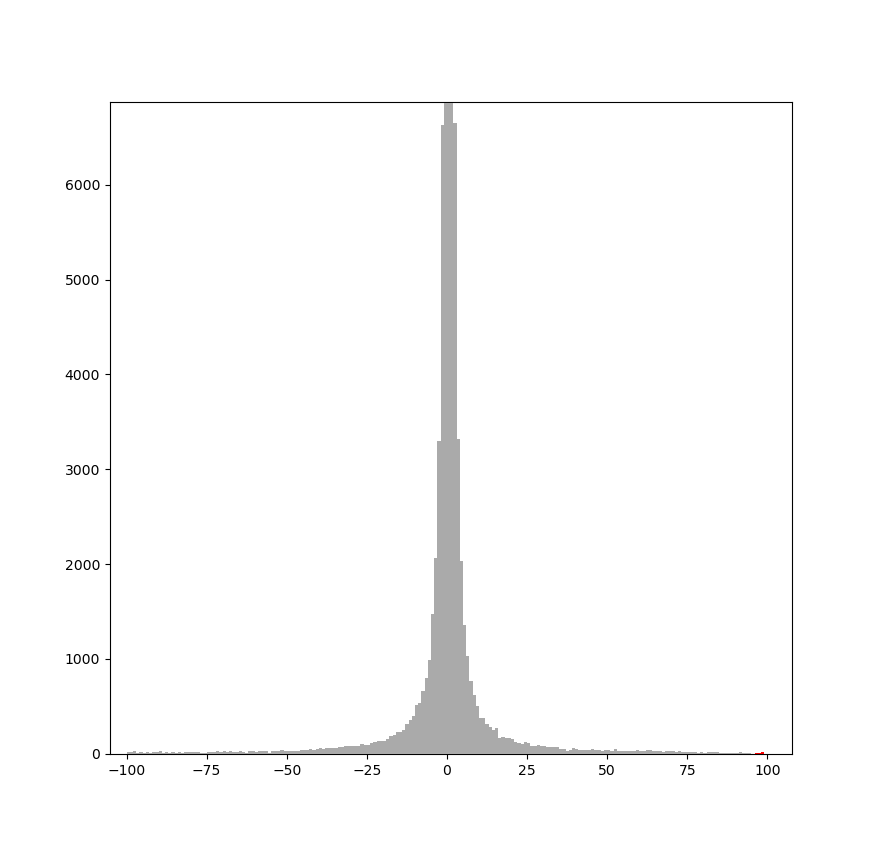
La alteración de la simetría del histograma es especialmente relevante en los métodos de esteganografía basados en modificaciones directas de los coeficientes. Si las modificaciones no se distribuyen de manera equilibrada entre los coeficientes positivos y negativos, la estructura estadística de la imagen comprimida se desvía de la que se esperaría en una imagen natural comprimida con JPEG, lo que facilita su detección. Por esta razón, muchas técnicas avanzadas de esteganografía en imágenes JPEG buscan preservar la simetría del histograma o aplicar modificaciones que minimicen su impacto en la distribución de los coeficientes.

En consecuencia, al diseñar métodos de modificación de coeficientes DCT, es fundamental considerar el impacto que estas alteraciones tendrán en la distribución estadística de los coeficientes. Mantener la simetría del histograma o diseñar modificaciones que respeten la estructura natural de los coeficientes DCT puede ser clave para reducir la detectabilidad de la información oculta.

Técnicas LSB

Las primeras técnicas de esteganografía para imágenes JPEG usaban LSB replacement o variantes de matching como las que hemos estudiado en Técnicas de incrustación: Incrustación de bits en el LSB. Sin embargo, esto producía un problema similar al que nos hemos encontrado al incrustar datos en regiones de silencio en audio, descrito en Técnicas de incrustación: Cómo evitar zonas detectables. La modificación de coeficientes DCT con valor cero mediante incrementos o decrementos de $\pm 1$ generaría patrones detectables con relativa facilidad, comprometiendo la seguridad del método.

Además, la alteración de los coeficientes DCT de valor cero puede provocar cambios perceptibles en la imagen reconstruida, lo que añade otro nivel de complejidad a la ocultación de información en el dominio transformado. Para abordar este problema de manera efectiva, es esencial emplear enfoques de esteganografía adaptativa, optimizando la selección de los coeficientes a modificar para minimizar la detectabilidad y preservar la calidad visual de la imagen.

Sin embargo, es importante señalar que en los primeros enfoques de esteganografía en imágenes JPEG, la esteganografía adaptativa aún no había sido desarrollada. En consecuencia, los primeros métodos de ocultación en este formato tuvieron que recurrir a soluciones ingeniosas para evitar los problemas producidos por la gestión de los ceros. A continuación, exploraremos algunas de estas estrategias.

Evitar la modificación de los coeficientes DCT de valor cero al incrustar información puede parecer una tarea sencilla, pero en realidad es un desafío complejo si se pretende hacerlo sin introducir anomalías estadísticas significativas. Supongamos que decidimos ignorar todos los coeficientes cuyo valor es cero. En ese caso, el receptor deberá hacer lo mismo al extraer el mensaje; de lo contrario, no podría recuperar correctamente la información. Esto implica una restricción adicional: el proceso de incrustación no debe generar nuevos ceros, ya que, si esto ocurre, dichos valores serán descartados en la extracción, lo que resultará en la pérdida de información.

Este problema, conocido como shrinkage, se ilustra fácilmente con un ejemplo. Si utilizamos LSB matching e intentamos incrustar información en un coeficiente con valor $1$ realizando una operación $-1$, o en un coeficiente $-1$ sumándole $1$, el resultado será un coeficiente con valor $0$. Dado que el receptor ignora estos ceros, los bits insertados en estas posiciones se perderían. Para solucionar este inconveniente, el conocido algoritmo de esteganografía F5 [westfeld:2001:f5] adoptó la siguiente estrategia: si durante la inserción se genera un coeficiente de valor cero, el proceso continúa y el mismo bit se inserta nuevamente en el siguiente coeficiente disponible. De esta manera, aunque se generen ceros adicionales y sean ignorados en la extracción, el receptor aún encontraría el bit incrustado en una posición posterior, evitando así la pérdida de información. Sin embargo, este método tiene una limitación importante, ya que reduce significativamente la capacidad de incrustación al requerir múltiples inserciones del mismo bit.

Otra forma de abordar el problema consiste en evitar generar ceros. Por ejemplo, en lugar de aplicar LSB matching de manera convencional, podríamos modificar los coeficientes de forma aleatoria con $+1$ o $-1$, excepto cuando $|x_i|= 1$. En este caso, si $x_i=1$, la modificación siempre sería con $+1$, mientras que si $x_i=-1$, se aplicaría $-1$. De esta manera, se evitaría la generación de nuevos ceros y se garantizaría la correcta extracción del mensaje.

No obstante, este enfoque introduce otro problema: altera la distribución del histograma de coeficientes DCT. En particular, las barras correspondientes a los valores $+1$ y $-1$ disminuirían en tamaño en comparación con las barras vecinas, mientras que las correspondientes a $+2$ y $-2$ aumentarían su frecuencia, generando una distorsión estadística detectable mediante análisis de estegoanálisis.

Por supuesto, existen otras opciones para incrustar información sin generar nuevos ceros. Pero todas ellas suelen alterar considerablemente el histograma de coeficientes DCT, lo que permite detectarlas con simples ataques estadísticos, como los ataques chi square [westfeld:2000].

Matrix embedding

Como hemos visto en el apartado anterior, la forma sencilla de preservar la distribución del histograma de coeficientes DCT sin introducir anomalías significativas implica la generación de nuevos ceros. Sin embargo, esto supone un desafío en la extracción del mensaje, ya que cualquier coeficiente convertido en cero durante la inserción se perdería. Para evitar este problema, es necesario volver a incrustar los bits afectados en coeficientes posteriores, una estrategia utilizada en el algoritmo F5 [westfeld:2001:f5]. No obstante, esta solución reduce considerablemente la capacidad del método, dado que algunos bits deben insertarse múltiples veces.

Una alternativa para mitigar esta pérdida de capacidad es el uso de matrix embedding, que permite incrementar la eficiencia de la incrustación, logrando ocultar una mayor cantidad de información con el mismo número de modificaciones en los coeficientes DCT.

A continuación vemos un ejemplo de implementación de algoritmo de tipo F5, en el que usamos matrix embedding con $p=3$ y realizamos una incrustación adicional cada vez que se genera un nuevo cero.

La parte de matrix embedding ya la hemos explicado anteriormente, por lo que nos centraremos en la función embed, que presenta cierta complejidad.

En primer lugar, el mensaje de texto se convierte en una secuencia de unos y ceros, los cuales serán incrustados uno a uno en la imagen. A continuación, se recorre la matriz de luminancia $Y$.

Un aspecto relevante es que se ignora el coeficiente DC, que corresponde al coeficiente de la esquina superior izquierda de cada bloque de $8 \times 8$. Esta omisión es común en muchos algoritmos de esteganografía, ya que dicho coeficiente influye en todo el bloque y puede generar diferencias notables respecto a los bloques vecinos, aumentando la detectabilidad del método.

Posteriormente, también se ignoran los coeficientes con valor cero, puesto que, como se ha explicado anteriormente, no conviene modificarlos.

A continuación, se leen coeficientes hasta obtener un grupo de $2^p-1$, almacenándolos en group, ya que esta cantidad es necesaria para aplicar el algoritmo de incrustación. Cada vez que se reúne un grupo de tres coeficientes, se determina cuál de ellos debe modificarse para incrustar el bit deseado, ajustando su valor absoluto, decrementándolo en una unidad. Este procedimiento permite conservar la forma del histograma, aunque ocasionalmente genere nuevos ceros.

Finalmente, si la modificación genera un nuevo cero, se elimina el último elemento del grupo para poder continuar. En caso contrario, la incrustación se considera válida y el proceso continúa.

import jpeg_toolbox as jt
import numpy as np
import random

P = 3
BLOCK_LEN = 2**P-1
M = np.array([
    [0, 0, 0, 1, 1, 1, 1],
    [0, 1, 1, 0, 0, 1, 1],
    [1, 0, 1, 0, 1, 0, 1]
])

def ME_embed(M, c, m):
    s = c.copy()
    col_to_find = (np.dot(M, c) - m) % 2
    for position, v in enumerate(M.T):
        if np.array_equal(v, col_to_find):
            s[position] = (s[position] + 1) % 2
            break
    return np.array(s)

def embed(img, message):
    dct_Y = img["coef_arrays"][0]

    message_bits = [
        int(bit) for byte in message.encode() for bit in format(byte, '08b')
    ]
    padding = (-len(message_bits)) % P
    message_bits += [0] * padding

    k = 0
    group = []
    for i in range(dct_Y.shape[0]):
        for j in range(dct_Y.shape[1]):
            if k+2 >= len(message_bits):
                break

            # Ignore DC
            if i % 8 == 0 and j % 8 == 0:
                continue

            # ignore zeros
            if dct_Y[i, j] == 0:
                continue

            group.append((i, j))
            if len(group) == BLOCK_LEN:
                m = message_bits[k:k+3]
                cover = np.array([int(dct_Y[a, b]) % 2 for a, b in group])

                stego = ME_embed(M, cover, m)
                idx = np.where(cover - stego != 0)[0]

                # No modifications needed
                if len(idx) == 0:
                    k += P
                    group = []
                    continue

                _i, _j = group[idx[0]]

                # Modify coef
                if dct_Y[_i, _j] < 0:
                    dct_Y[_i, _j] += 1
                else:
                    dct_Y[_i, _j] -= 1

                # Shrinkage
                if dct_Y[_i, _j] != 0:
                    k += P
                    group = []
                else:
                    del group[idx[0]]

    img["coef_arrays"][0] = dct_Y
    return img

img = jt.load("image.jpeg")
message = "Hidden text"
stego_img = embed(img, message)
jt.save(stego_img, "image_stego.jpeg")

A continuación, se proporciona el código Python para la extracción del mensaje oculto. El procedimiento resulta más simple que el usado en la incrustación. En primer lugar, se recorre la matriz de luminancia $Y$ siguiendo el mismo orden utilizado durante la inserción del mensaje. Durante este recorrido, se descartan tanto los coeficientes DC como aquellos con valor cero. Después, los coeficientes válidos se agrupan en bloques de $2^p - 1$ elementos, utilizando cada grupo para extraer $p$ bits del mensaje oculto. Finalmente, la secuencia de bits obtenida se convierte en el mensaje de texto original.

Igual que en apartados anteriores, no hemos establecido un mecanismo para saber cuándo el mensaje ha sido extraído al completo, por lo que en el ejemplo sacamos directamente los $88$ bits que sabemos que tiene el mensaje. Sin embargo, como también se comentó en apartados anteriores, la forma correcta de hacerlo sería usando una cabecera al principio que nos diga la longitud del mensaje, o incrustar una marca de fin de mensaje.

import jpeg_toolbox as jt
import numpy as np

class EndLoop(Exception):
    pass

P = 3
BLOCK_LEN = 2**P-1
M = np.array([
    [0, 0, 0, 1, 1, 1, 1],
    [0, 1, 1, 0, 0, 1, 1],
    [1, 0, 1, 0, 1, 0, 1]
])

def ME_extract(M, s):
    return np.dot(M, s) % 2

def extract(img, msglen):
    dct_Y = img["coef_arrays"][0]

    l = msglen + (-msglen) % P
    num_blocks = (l // 3)

    message = []
    p = 3
    group_size = 2**p - 1
    group = []
    try:
        for i in range(dct_Y.shape[0]):
            for j in range(dct_Y.shape[1]):

                # Ignore DC
                if i % 8 == 0 and j % 8 == 0:
                    continue
                # ignore zeros
                if dct_Y[i, j] == 0:
                    continue

                group.append((i, j))
                if len(group) == group_size:
                    stego = np.array([int(dct_Y[a, b]) % 2 for a, b in group])
                    m = ME_extract(M, stego)
                    message += m.tolist()
                    group = []
                    if len(message) >= msglen:
                        raise EndLoop

    except EndLoop:
        pass

    message_bits = ''.join(map(str, message))
    message = ''.join(
        chr(int(message_bits[i:i+8], 2))
        for i in range(0, len(message_bits), 8)
    )

    return message

img = jt.load("image_stego.jpeg")
extracted_message = extract(img, 88)
print(extracted_message)

Wet Paper Codes

En el apartado anterior hemos analizado el problema que representa la aparición de nuevos coeficientes de valor cero en esteganografía JPEG, así como la solución propuesta por el algoritmo F5 [westfeld:2001:f5]. Aunque efectiva, esta solución dista de ser óptima, ya que requiere la reinserción de ciertos bits, lo que reduce la capacidad del método de esteganografía.

Una alternativa más eficiente consiste en utilizar técnicas de incrustación adaptativa, que permiten evitar explícitamente los coeficientes cero, sin necesidad de reinserciones. Ya hemos explorado cómo funcionan estas técnicas en capítulos anteriores. Una opción particularmente eficaz es el uso de Syndrome Trellis Codes, disponibles a través de la librería pySTC. En este caso, es necesario definir una función de coste que penalice fuertemente los coeficientes de valor cero y asigne un coste bajo al resto. Este procedimiento es relativamente sencillo y ha sido tratado previamente en el capítulo mencionado.

Definimos la función de coste $C(i,j)$ para un coeficiente DCT $x_{i,j}$ como:

Esta función penaliza fuertemente la modificación de coeficientes cuyo valor sea cero, asignándoles un coste infinito. En cambio, permite modificar libremente el resto de coeficientes, asignándoles un coste nulo, independientemente de su valor.

Podemos escribir la función de cálculo de costes de la siguiente manera, en la que asignamos un coste alto, en lugar de infinito:

import numpy as np

def cost(coeffs, high_cost=1e10):
    cost = np.zeros_like(coeffs, dtype=float)
    cost[coeffs == 0] = high_cost
    return cost

Esta forma de incrustar elimina el problema del shrinkage que hemos estudiado en el apartado anterior, por ello se la conoce como non-shrinkage F5 o nsF5 [Fridrich:2007:nsF5].

Aunque esta estrategia resulta efectiva para resolver el problema planteado por F5, no se ajusta del todo a los principios de la esteganografía adaptativa en imágenes JPEG. El objetivo, como ya se ha discutido en otros capítulos, es seleccionar aquellas regiones de la imagen donde la incrustación resulta más difícil de detectar. Este enfoque será tratado con mayor profundidad en el siguiente apartado.

Incrustación adaptativa

En capítulos previos hemos estudiado cómo construir una función de coste que se adapte a aquellas zonas de la imagen que son más difíciles de modelar estadísticamente, y que, por tanto, son también las más adecuadas para ocultar información sin ser detectados. Lo aprendido sigue siendo válido, ya que el análisis de la imagen descomprimida continúa siendo aplicable en este contexto.

En otras palabras, podemos modificar los coeficientes DCT, descomprimir la imagen y estudiar cómo se ven afectados los píxeles resultantes, con el fin de determinar si dichas modificaciones han alterado zonas que preferiríamos no modificar. Esto introduce una capa adicional de complejidad, ya que no solo es necesario calcular el coste en el dominio DCT, sino también evaluar el impacto de estas modificaciones tras la descompresión.

El principal inconveniente de este enfoque es su elevado coste computacional. Si para cada bloque de $8 \times 8$ coeficientes debemos realizar una descompresión para evaluar su efecto sobre los píxeles, el número de operaciones se incrementa considerablemente. Este problema se agrava si todos estos cálculos se realizan en Python, ya que el rendimiento puede volverse un factor limitante importante.

Por este motivo, este tipo de esteganografía se enfrenta más a limitaciones prácticas que a problemas teóricos. Es decir, aunque en teoría pueden existir métodos más eficaces para definir funciones de coste más precisas, su aplicación real puede verse restringida por el rendimiento de la implementación.

Por tanto, no solo es importante diseñar funciones de coste óptimas, sino también combinarlas con herramientas que permitan mejorar la eficiencia computacional. Una opción recomendable es el uso de la librería Numba, que permite la compilación just-in-time de determinadas partes del código, acelerando significativamente su ejecución.

Un algoritmo especialmente efectivo que muestra cómo calcular una función de coste en JPEG es J-UNIWARD [Holub:2014:uniward]. Este algoritmo excede los objetivos de este libro, pero vamos a estudiar las ideas básicas que hay tras él. El lector puede visitar el siguiente enlace, en el que se proporcionan diferentes implementaciones de J-UNIWARD:

https://github.com/daniellerch/stegolab/tree/master/J-UNIWARD

Para el aprendizaje se recomienda usar j-uniward.py que es una implementación para imágenes en escala de grises. Una vez comprendida esta versión, se puede continuar con j-uniward-color.py para ver cómo trabajar con imágenes en color. Como hemos comentado anteriormente, el proceso puede ser costoso computacionalmente, por ello en j-uniwardfast-color.py se muestra cómo usar Numba para acelerar la ejecución.

La idea principal detrás de J-UNIWARD consiste en calcular el impacto que supone la modificación de cada coeficiente DCT en los píxeles. Para ello, calcula el coste que suponen estas modificaciones en la imagen descomprimida, por separado:

import scipy.fftpack
import numpy as np

def idct2(a):
    return scipy.fftpack.idct(scipy.fftpack.idct(a, axis=0, norm='ortho'),
                              axis=1, norm='ortho')

# ...
spatial_impact = {}
for i in range(8):
    for j in range(8):
        test_coeffs = np.zeros((8, 8))
        test_coeffs[i, j] = 1
        spatial_impact[i, j] = idct2(test_coeffs) * jpg["quant_tables"][0][i, j]
# ...

De esta manera puede aplicar una función de coste en la imagen descomprimida. La que usa J-UNIWARD es diferente de la función HILL [Li:2014:hill] que estudiamos anteriormente, pues usa filtros basados en wavelets pero el principio es el mismo:

import scipy.signal

# ...
wavelet_impact = {}
for f_index in range(len(F)):
    for i in range(8):
        for j in range(8):
            wavelet_impact[f_index, i, j] = scipy.signal.correlate2d(
                spatial_impact[i, j], F[f_index],
                mode='full', boundary='fill',
                fillvalue=0.0
            )
# ...

En resumen, la idea general de la esteganografía adaptativa en JPEG consiste en crear una función que le asigne un coste a cada coeficiente, de manera que se tenga en cuenta el impacto que tendrá la modificación de ese coeficiente en la imagen descomprimida. Con esta función de coste ya se puede aplicar STC sobre los coeficientes.

Compresión en plataformas

Muchas redes sociales, aplicaciones de mensajería, foros, etc., aplican automáticamente compresión con pérdida a las imágenes que los usuarios suben, principalmente en formato JPEG. Esta práctica tiene como objetivo reducir el tamaño de los archivos para optimizar el uso de almacenamiento y acelerar la transmisión de contenido. Aunque desde el punto de vista de la infraestructura resulta beneficiosa, para la esteganografía representa una amenaza directa: cualquier técnica que dependa de los valores exactos de píxeles o de coeficientes DCT puede quedar inutilizada si la imagen es recomprimida por la plataforma.

Cuando se incrusta un mensaje en una imagen sin comprimir —por ejemplo, en un archivo PNG o BMP—, y dicha imagen es transformada automáticamente a JPEG por la plataforma, se pierde la información oculta en el LSB de los píxeles. La transformación al dominio DCT, seguida de la cuantización, altera completamente los datos sobre los que se realizó la incrustación, destruyendo el mensaje. Pero incluso si la imagen ya estaba en formato JPEG, la recompresión puede igualmente arruinar el contenido oculto. Esto ocurre si la calidad JPEG aplicada por la plataforma es diferente de la utilizada por el emisor al crear la imagen. En ese caso, los coeficientes DCT serán alterados por una nueva cuantización, eliminando o distorsionando los bits que contenían el mensaje.

Para mitigar este problema, una técnica sencilla pero eficaz consiste en aplicar de antemano la misma compresión que la plataforma aplicará. Si se conoce la calidad JPEG que emplea una red social determinada, es posible comprimir previamente la imagen con esa misma configuración. A continuación, se puede aplicar sobre ella cualquier técnica de esteganografía diseñada para imágenes JPEG, como las descritas en los apartados anteriores. De este modo, la compresión aplicada por la plataforma no afectará a los coeficientes originales y, por tanto, el mensaje oculto permanecerá. Por ejemplo, si se ha determinado experimentalmente que una plataforma concreta utiliza una calidad JPEG cercana al 85\%, el usuario puede convertir primero su imagen a JPEG con esa calidad, y luego aplicar sobre el archivo resultante un método como nsF5 [Fridrich:2007:nsF5] o J-UNIWARD [Holub:2014:uniward].