Códigos de Hamming Ternarios en Esteganografía

A continuación se presenta una técnica de incrustación de información de tipo matrix embedding basada en códigos de Hamming ternarios.

1. Introducción
2. Códigos de Hamming ternarios
3. Eficiencia y distorsión
4. Ejemplo en Python
5. Codificación del mensaje
6. Implementación completa en Python
7. Referencias

Introducción

En el artículo Códigos de Hamming binarios en esteganografía hemos visto cómo ocultar información con códigos binarios usando operaciones $+1$ y $-1$ sobre el valor de los bytes. Sin embargo, con los códigos binarios solo estamos interesados en el valor del LSB, por lo que no es importante si la operación que realizamos es $+1$ o es $-1$, lo que nos suele llevar a elegir aleatoriamente.

Teniendo en cuenta que las operaciones que realizamos son de tipo $\pm 1$ (LSB matching), podríamos decir que no estamos aprovechando al máximo este sistema de inserción. Si en lugar de reemplazar el bit menos significativo de cada byte, optamos por realizar una operación $\pm 1$ estamos trabajando con tres posibles valores: +1, -1 y 0 (dejamos el valor como estaba). Con lo que, en lugar de usar un código binario, podemos usar un código ternario.

La teoría detrás de los códigos de Hamming ternarios es la misma que la de los códigos binarios. La única diferencia es que en lugar de realizar operaciones módulo $2$, para quedarnos con el LSB, las haremos módulo 3, para quedarnos con un valor de $0$, $1$ o $2$.

Por otra parte, para ocultar información en un byte necesitaremos trabajar con el valor del byte módulo $3$. Es decir, para un código ternario, un byte con valor 233 correspondería aun valor ternario $235\pmod 3 = 2$.

Códigos de Hamming Ternarios

Veamos un ejemplo de incrustación. Vamos a usar $p=3$, es decir, que queremos insertar un símbolo ternario por cada modificación. Para ello, trabajaremos con grupos de $ \frac{n^p-1}{n-1} = \frac{3^3-1}{2} = 13$ bytes.

Nótese que en lugar de usar $2^p-1$ como en los códigos binarios, estamos usando $\frac{3^3-1}{2}$. Ambos casos proceden de la siguiente fórmula que nos permite calcular el tamaño de los grupos de bytes en los que vamos a ocultar la información:

Supongamos que después de seleccionar un grupo de 13 bytes del medio en el que queremos incrustar el mensaje, y de realizar la operación módulo 3, obtenemos el siguiente vector cover:

Recordemos que también necesitamos una matriz que contenga en sus columnas todas las posibles combinaciones, excepto el vector de ceros. En este caso, además, tendremos que eliminar los vectores linealmente dependientes.

Una opción sería la siguiente:

Y finalmente, necesitamos también el mensaje que queremos ocultar. Ocultemos por ejemplo:

Si calculamos el mensaje oculto en nuestro vector $c$ vemos que es:

Lógicamente, no es el que queremos ocultar. Buscamos pues qué columna de M es la responsable:

Es la columna 9 de la matriz M. Por lo que, para obtener el vector stego $s$ tenemos que sumar 2 (o restar 1) al valor de esa posición en el vector $c$:

Podría darse el caso de que, en la matriz M, no encontrásemos la columna que buscamos, pero sí una combinación lineal. En este caso sumaríamos 1 (o restaríamos 2).

Cuando el receptor del mensaje obtenga el vector stego del medio, podrá extraer el mensaje mediante:

Eficiencia y distorsión

En lugar de usar técnicas de inserción $\pm 1$, podemos usar técnicas $\pm k$, siendo $k$ cualquier valor que nos interese. Sin embargo, cuanto mayor sea $k$, mayor será la distorsión introducida, por lo que puede no ser apropiado seleccionar valores demasiado grandes.

Si hemos usado códigos ternarios para la inserción $\pm 1$, con la inserción $\pm 2$ tendremos que usar códigos quinarios, puesto que tenemos cinco operaciones posibles: -2, -1, 0, +1 y +2.

En este caso el proceso sería es el mismo que antes, cambiando el valor del módulo a $n=5$. Si usamos, por ejemplo, $p=3$ tendremos que usar grupos de $\frac{n^p-1}{n-1}=\frac{5^3-1}{4}=31$ bytes.

La misma idea serviría para otros valores de $k$ y $n$.

En la siguiente gráfica puede verse una comparativa de diferentes códigos n-arios. Para calcular el payload usaremos:

${\alpha}_p = \frac{p \log_2 n}{(n^p-1)/(n-1)}$

Y para calcular la eficiencia:

$e_p = \frac{p \log_2 n}{1-n^{-p}}$

Esto nos permite dibujar una gráfica para ver la eficiencia respecto el payload para diferentes valores de $p$ y $n$. Para una mejor visualización, se usa el inverso del payload ($\alpha^{-1}$).

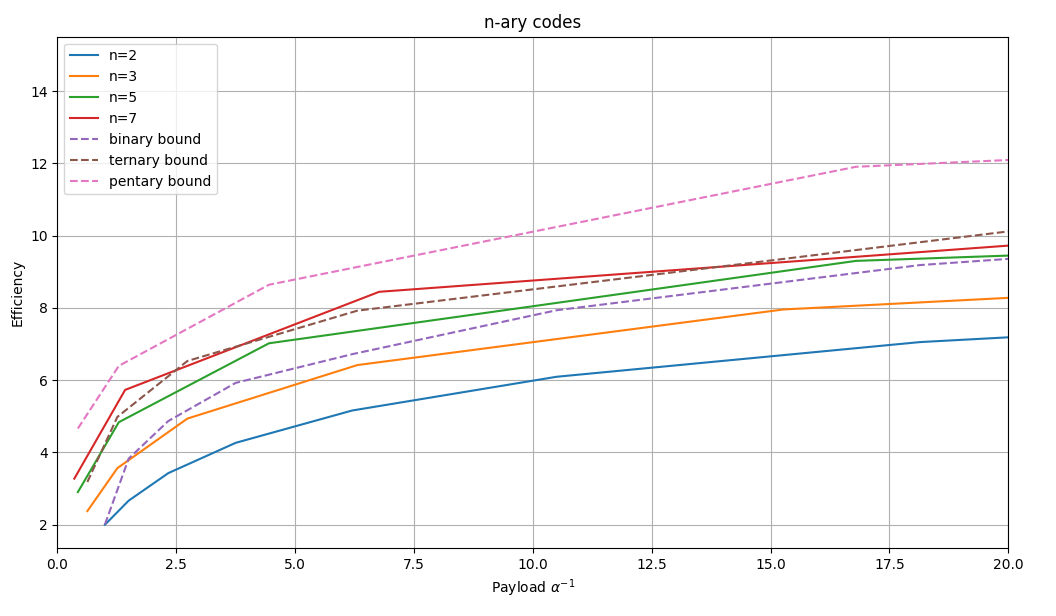
Como se puede ver en las gráficas, cuanto mayor es $n$ mayor es la eficiencia del método. Sin embargo, aumentar demasiado $n$ implica trabajar con valores de $k$ quizás demasiado grandes, que pueden distorsionar mucho el medio y hacer que el método esteganográfico sea más detectable.

Sin embargo, hay algo que no se puede pasar por alto. La distorsión introducida por los códigos binarios es la misma que la introducida por los códigos ternarios, puesto que en ambos casos realizamos únicamente operaciones $+1$ y $-1$. La diferencia es que, mientras que en los códigos binarios elegimos una u otra aleatoriamente, en los códigos ternarios esta decisión forma parte del código. Por lo tanto, el uso de los códigos ternarios nos ofrecerá más capacidad para el mismo grado de distorsión.

En la gráfica también se puede ver el límite teórico para cada tipo de código. Como se puede observar, los códigos usados no alcanzan la máxima capacidad teórica.

Ejemplo en Python

Veamos el código Python que nos permite realizar estas operaciones. Primero necesitamos preparar la matriz $M$:

M = np.array([
    [1, 0, 0, 0, 1, 1, 1, 0, 2, 1, 2, 1, 1],
    [0, 1, 0, 1, 0, 1, 1, 1, 0, 2, 1, 2, 1],
    [0, 0, 1, 1, 1, 0, 1, 2, 1, 0, 1, 1, 2]
])

Para incrustar el mensaje $m$ en el vector cover $c$ únicamente tenemos que buscar la posición de $Mc-m$ en la matriz $M$ y modificarla:

import numpy as np
def embed(M, c, m, n):
    s = c.copy()
    col_to_find = (M.dot(c)-m)%n
    position = 0
    for v in M.T:
        if np.array_equal(v, col_to_find):
            s[position] = (s[position] - 1)%n
            break
        elif np.array_equal((v*2)%n, col_to_find):
            s[position] = (s[position] + 1)%n
            break
        position += 1
    return s

Para extraer el mensaje incrustado bastará con realizar la operación $Ms$:

def extract(M, s, n):
    return M.dot(s)%n

Repitamos ahora el ejemplo usando Python:

m = [2, 0, 2]
c = [0,1,0,0,2,1,2,2,2,0,1,0,2]
s = embed(M, c, m, 3)
new_m = extract(M, s, 3)

>>> new_m
array([2, 0, 2])

Codificación del mensaje

Todo parece indicar que es más apropiado usar un código ternario que un código binario, puesto que nos da una capacidad más alta para el mismo nivel de distorsión. Sin embargo, los ordenadores representan la información en binario, por lo que usar un código ternarario requiere un poco de trabajo extra.

Concretamente, necesitamos poder pasar de binario a ternario, y biceversa. Esta funcionalidad nos la proporciona la función base_repr() de la librería Numpy.

Veamos un ejemplo. Primero convertiremos de binario a un número decimal:

>>> binary_string = "1010101011111111101010101010010"
>>> num = int(binary_string, 2)
>>> num

1434441042

A continuación, representaremos este número en base 3:

>>> ternary_string = np.base_repr(num, base=3)
>>> ternary_string

'10200222011011012000'

El proceso inverso se realiza de forma similar:

>>> num = int(ternary_string, 3)
>>> binary_string = np.base_repr(num, base=2)
>>> binary_string

'1010101011111111101010101010010'

Implementación completa en Python

En el enlace de GitHub se proporciona una implementación completa, que incluye la codificación y descodificación del mensaje, antes y después de la inserción.

A continuación, se muestra un ejemplo en el que escondemos datos en una imagen:

import imageio

cover = imageio.imread("image.png")
message = "Hello World".encode('utf8')
hc = HC3(3)
stego = cover.copy()
stego[:,:,0] = hc.embed(cover[:,:,0], message)
imageio.imsave("stego.png", stego)

stego = imageio.imread("stego.png")
extracted_message = hc.extract(stego[:,:,0])
print("Extracted message:", extracted_message.decode())

Referencias

1. Fridrich, J. (2009). Steganography in Digital Media: Principles, Algorithms, and Applications. Cambridge University Press.