A continuación se presenta una técnica de incrustación de información de tipo matrix embedding basada en códigos de Hamming binarios.
- Introducción
- Códigos de Hamming binarios
- Eficiencia
- Ejemplo en Python
- Implementación completa en Python
- Referencias
Introducción
En esteganografía decimos que la eficiencia de la inserción es 1 cuando necesitamos hacer una modificación cada vez que incrustamos un bit. Sin embargo, Cuando ocultamos información en el LSB (ver Esteganografía LSB en imágenes y audio) la eficiencia de la inserción es de 2. Esto es así debido a que, estadísticamente, la mitad de los bytes en los que queremos ocultar información ya tendrán como valor del LSB el bit del mensaje que queremos incrustar. Por lo tanto, no será necesario modificarlos. Así pues, estaremos incrustando un bit en cada byte, pero solo estaremos modificando la mitad de los bytes. En consecuencia, la eficiencia será de 2 bits por modificación.
Esta eficiencia puede mejorarse fácilmente con un sencillo truco. Veamos cómo funciona.
Vamos a ocultar información en grupos de tres bytes:
| A | B | C |
y vamos a usar esta fórmula para ocultar el primer bit:
y esta fórmula para ocultar el segundo:
Aquí $LSB()$ hace referencia al bit menos significativo del píxel y $\oplus$ a una operación XOR.
Aplicar este método es muy sencillo. Si $M_1$ y $M_2$ ya tienen los valores que queremos ocultar, no tenemos que hacer nada. Si ninguno de los valores de $M_1$ y $M_2$ coincide cambiaremos el LSB de $B$. Si $M_1$ coincide pero $M_2$ no, cambiaremos el LSB de $C$ y si $M_2$ coincide pero $M_1$ no, cambiaremos el valor de $A$. Con esta sencilla técnica podemos ocultar dos bits modificando solo uno.
Veamos un ejemplo. Tenemos los siguientes píxeles:
| 10010100 | 10010101 | 10010111 |
Si queremos ocultar $00$ un posible resultado es:
| (+1) 10010101 | 10010101 | 10010111 |
Si queremos ocultar $01$ una opción será:
| 10010100 | (-1) 10010100 | 10010111 |
Si queremos ocultar $10$, no tenemos que realizar cambios:
| 10010100 | 10010101 | 10010111 |
Y finalmente, si queremos ocultar $11$ un posible resultado será:
| 10010100 | 10010101 | (-1) 10010110 |
Hay cuatro opciones $00$, $01$, $10$ y $11$. Para una de cada cuatro opciones, no será necesario realizar ninguna modificación, mientras que para las otras tres modificaremos un solo bit. Por lo tanto, modificaremos un bit cada 3/4 de los casos. Puesto que cada una de estas modificaciones nos permite incrustar dos bits, tenemos una eficiencia de $\frac{2}{3/4}=2.66$. Esta eficiencia es superior a la de la esteganografía LSB, que era de $2$.
Códigos de Hamming binarios
La idea propuesta en el apartado anterior puede generalizarse usando una técnica conocidad como matrix embedding mediante Códigos de Hamming. Esta técnica nos permite ocultar $p$ bits en un bloque de $2^p-1$ bits, modificando un solo bit.
Lo primero que vamos a necesitar es una matriz que contenga todas las combinaciones de vectores binarios de $p$ elementos, excepto el vector de ceros. Por ejemplo, si queremos usar $p=3$, una posible matriz será la siguiente:
Para ocultar $p$ bits necesitamos un grupo de $2^p-1$ bits. Este grupo lo obtendremos del medio en el que queremos ocultar la información y lo llamaremos vector cover, denotado por $c$.
Podemos calcular el mensaje que oculta de forma “natural” un vector cover realizando la siguiente operación:
Es importante tener en cuenta que trabajamos con bits, es decir, que todas las operaciones que realizamos son operaciones módulo 2.
Aunque puede darse el caso de que el mensaje $m$ coincida con los bits que queremos incrustar, no ocurrirá siempre. Para poder modificar de forma adecuada el vector $c$ para que oculte nuestro mensaje, lo primero que haremos es restar el mensaje $m$ que queremos ocultar de $Mc$:
La posición del vector $v$ en la matriz $M$ nos dirá qué bit de $c$ tenemos que modificar (obteniendo el vector stego $s$) para que al realizar la operación de extracción $Ms$ obtengamos el mensaje que queremos ocultar.
Veamos un ejemplo sencillo con $p=3$ en el que vamos a ocultar el mensaje $m=(1,1,0)$.
Dado que $p=3$ necesitaremos ocultar nuestro mensaje en grupos de $2^p-1=7$ bits, por lo que para cada incrustación necesitaremos un vector cover $c$ de 7 bits. Obtendremos dicho vector del medio y nos quedaremos con su LSB.
Supongamos que los bytes extraídos del medio son los siguientes:
| 11011010 | 11011011 | 11011011 | 11011010 |
| 11011011 | 11011010 | 11011010 |
Nos quedamos con los LSB:
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
Por lo que nuestro vector $c$ será:
Calculamos el mensaje que oculta este vector:
Pero este no es el mensaje que queremos ocultar, puesto que queremos ocultar $m=(1,1,0)$. Por lo tanto tenemos que averiguar cómo modificar $c$ de manera que el resultado de la operación oculte nuestro mensaje. Es decir, necesitamos obtener la versión stego $s$ de nuestro vector $c$ para que $m = Mc = (1, 1, 0)$.
Primero tendremos que realizar la operación $Mc-m$ para localizar la posición de $c$ que tenemos que modificar para obtener $s$.
que corresponde a la segunda columna de $M$:
Esto significa que tenemos que cambiar el segundo bit de $c$ para obtener el vector stego $s$.
De esta manera, la operación de extracción dará como resultado nuestro mensaje:
En este punto, únicamente tenemos que trasladar esta modificación al valor inicial de los bytes extraídos del medio. Es decir, convertimos:
| 11011010 | 11011011 | 11011011 | 11011010 |
| 11011011 | 11011010 | 11011010 |
en:
| 11011010 | 11011010(-1) | 11011011 | 11011010 |
| 11011011 | 11011010 | 11011010 |
Aunque hemos realizado una operación -1, también nos habría servido una operación +1, puesto que lo que nos interesa es el valor del LSB:
| 11011010 | 11011100(+1) | 11011011 | 11011010 |
| 11011011 | 11011010 | 11011010 |
Eficiencia
Cuanto más grande sea $p$, más información podremos ocultar con menos modificaciones. Pero si usamos un $p$ demasiado grande nos encontraremos con que los grupos son tan grandes que nos quedamos rápidamente sin bytes en los que esconder información. Por ejemplo, en una imagen de 512x512 píxeles podemos esconder 18 bits modificando un solo bit. Sin embargo, ya no podemos ocultar nada más. Conviene pues seleccionar un $p$ adecuado, que nos permita ocultar información sin modificar mucho el medio, pero que al mismo tiempo nos ofrezca una capacidad aceptable.
Nos interesa tener en cuenta dos parámetros. El primero es el payload, es decir, qué porcentaje de información podemos almacenar por byte modificado. Esto podemos calcularlo con la siguiente fórmula:
Por ejemplo, si usamos $p=3$, necesitaremos grupos de $2^3-1=7$ valores. Lo que nos da una capacidad de $0.429$ bits por byte (píxel, muestra de audio, etc).
El siguiente parámetro que nos interesa es la eficiencia de la inserción, que podemos calcular como:
Siguiendo con nuestro ejemplo, la eficiencia para $p=3$ es de $3.429$. Superior a nuestro ejemplo inicial, que tenía una eficiencia de $2.66$.
En el siguiente gráfico podemos ver la relación entre el payload y la eficiencia. En realidad, para una mejor visualización, se usa el inverso del payload ($\alpha^{-1}$).
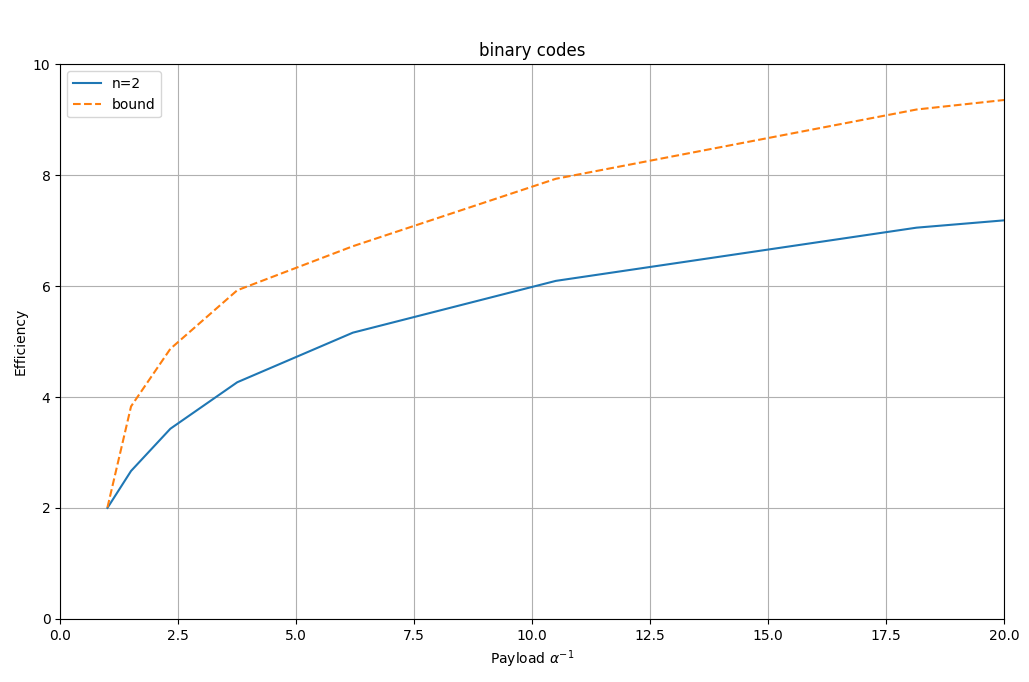
Como se puede ver en la gráfica, la mayor eficiencia se consigue con payloads muy pequeños ($\alpha^{-1}$ muy grande).
En la gráfica también se muestra el límite teórico de los códigos binarios. Como se puede observar, no se alcanza el límite teórico.
Ejemplo en Python
Veamos ahora como realizar estas operaciones usando el lenguaje de programación Python.
Lo primero que necesitamos es la matriz $M$:
import numpy as np
M = np.array([
[0, 0, 0, 1, 1, 1, 1],
[0, 1, 1, 0, 0, 1, 1],
[1, 0, 1, 0, 1, 0, 1]
])
Para incrustar el mensaje $m$ en el vector cover $c$ únicamente tenemos que buscar la posición de $Mc-m$ en la matriz $M$ y modificarla:
def embed(M, c, m):
s = c.copy()
col_to_find = (M.dot(c)-m)%2
position = 0
for v in M.T:
if np.array_equal(v, col_to_find):
s[position] = (s[position] + 1) % 2
break
position += 1
return s
Para extraer el mensaje incrustado bastará con realizar la operación $Ms$:
def extract(M, s):
return M.dot(s)%2
Repitamos el ejemplo anterior, ahora usando Python:
m = [1, 1, 0]
c = np.array([
0b11011010, 0b11011011, 0b11011011, 0b11011010,
0b11011011, 0b11011010, 0b11011010
])%2
s = embed(M, c, m)
new_m = extract(M, s)
>>> new_m
array([1, 1, 0])
Implementación completa en Python
En el enlace de GitHub se proporciona una implementación completa, que incluye la codificación y descodificación del mensaje, antes y después de la inserción.
A continuación, se muestra un ejemplo en el que escondemos datos en una imagen:
import imageio
cover = imageio.imread("image.png")
message = "Hello World".encode('utf8')
hc = HC(3)
stego = cover.copy()
stego[:,:,0] = hc.embed(cover[:,:,0], message)
imageio.imsave("stego.png", stego)
stego = imageio.imread("stego.png")
extracted_message = hc.extract(stego[:,:,0])
print("Extracted message:", extracted_message.decode())
Referencias
- Fridrich, J. (2009). Steganography in Digital Media: Principles, Algorithms, and Applications. Cambridge University Press.