In this article we are going to talk about how to detect tools that use the LSB replacement or LSB replacement technique in uncompressed images. To do this, we are going to use the steganalysis tool Aletheia.
- How LSB replacement works
- OpenStego
- OpenPuff
- Initial exploration
- Structural steganalysis
- Brute force attack on OpenStego
- LSB matching: a simple alternative to LSB replacement
How LSB replacement works
In uncompressed images represented as bitmaps, it is common to represent each pixel by three bytes: the R byte, which indicates the amount of red, the G byte, which indicates the amount of green and the B byte, which indicates the amount of blue. Since the modification of these bytes by a few units is not perceptible to the human visual system, this can be exploited to hide information.
Since each byte is made up of 8 bits, a simple way to hide information without altering the value of the pixel too much is to substitute the value of the least significant bit (LSB or Least Significant Bit ), by the value of the bit of the message that we want to hide.
Suppose that the first three pixels of an RGB image have the following values:
| R | G | B |
| 160 | 60 | 53 |
| 128 | 111 | 43 |
| 84 | 125 | 125 |
If we represent their values in binary, we get:
| R | G | B |
| 10100000 | 00111100 | 00110101 |
| 10000000 | 01101111 | 00101011 |
| 01010100 | 01111101 | 01111101 |
As an example, we are going to hide the letter ‘A’ in ASCII code. That is, the binary value 01000001. To hide this information in the first three pixels, we only have to replace the value of the LSB with the value of the message:
| R | G | B |
| 10100000 | 00111101 | 00110100 |
| 10000000 | 01101110 | 00101010 |
| 01010100 | 01111101 | 01111101 |
Unfortunately, this type of insertion is not very secure and there are many attacks that exploit it. The first of these attacks are from the late 1990s, although they evolved significantly in later years. Currently, these types of attacks, known as structural attacks, are good enough to consider to LSB replacement a steganographic technique to avoid.
Curiously, there are still many tools that implement LSB replacement. For Example OpenStego and OpenPuff, which we analyze in this article.
OpenStego
OpenStego is an open source tool developed in Java to hide messages in images (steganography and watermarking). Next, we are going to analyze this tool in its version v0.8.0.
To perform the analysis we are going to download an image from the Waterloo repository. Specifically the “Monarch” image. Next, we will convert it to PNG, since OpenStego does not support the TIFF format.
wget http://links.uwaterloo.ca/Repository/TIF/monarch.tif
convert monarch.tif monarch.png
We get this image:

We are going to hide a 20000 byte message. We generate the message with the following command:
dd if=/dev/urandom of=secret.txt bs=1 count=20000
20000+0 registros leídos
20000+0 registros escritos
20000 bytes (20 kB, 20 KiB) copied, 0,0451231 s, 443 kB/s
Next, we will use OpenStego to hide the message.
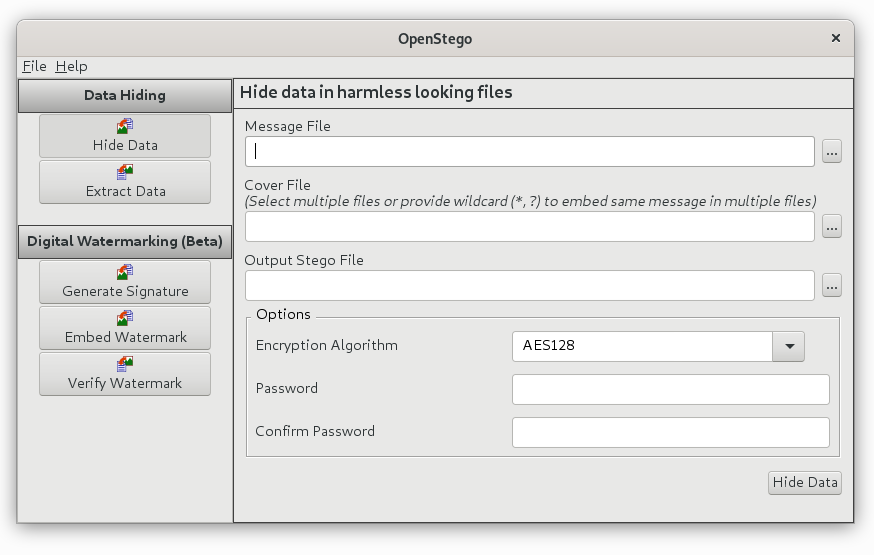
Leaving an image stego indistinguishable from the original for the human eye.

OpenPuff
OpenPuff is a free tool for hiding information on different types of media. Next, we are going to analyze this tool in its version v4.0.1, when the images in which the information is hidden are uncompressed.
To perform the analysis we will download an image from the Waterloo repository. Specifically the image “Peppers”. And then we will convert it to PNG, since OpenPuff does not support the TIFF format.
wget http://links.uwaterloo.ca/Repository/TIF/peppers3.tif
convert peppers3.tif peppers3.png
We get this image:

We will hide a message of about 5000 bytes, which is the maximum that OpenPuff allows us to save when we use the minimum and safest payload (12.5%). We generate the message with the following command:
dd if=/dev/urandom of=secret.txt bs=1 count=5000
5000+0 registros leídos
5000+0 registros escritos
5000 bytes (5,0 kB, 4,9 KiB) copied, 0,0106255 s, 471 kB/s
Next, we will use OpenPuff to hide the message.
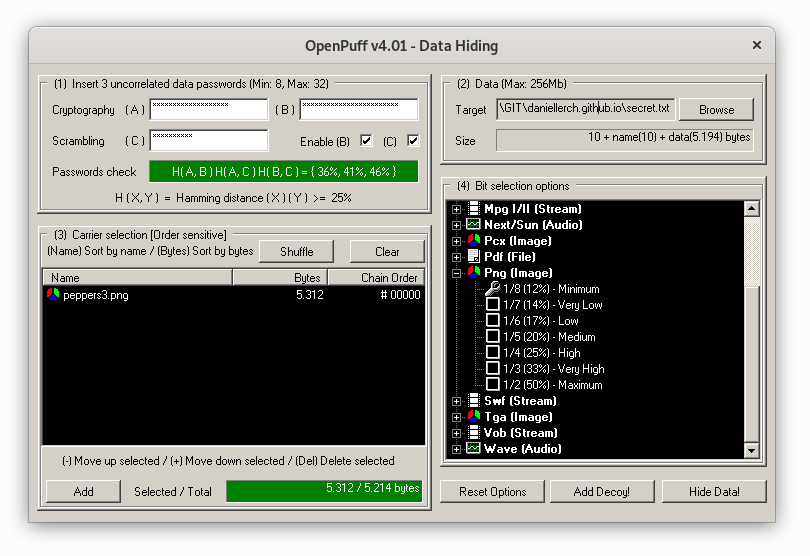
We get the following stego image:

Initial exploration
To know what attacks we can carry out, it is necessary to know what insertion technique was used. OpenStego uses LSB replacement so we can use all the techniques that Aletheia implements to attack LSB replacement.
We can see that OpenStego does indeed use LSB replacement by comparing an original image with an image with a hidden message. Aletheia offers us the command print-diffs that shows us the differences between the pixels. With this command we can see what happens when hiding a message.
$ ./aletheia.py print-diffs monarch.png monarch_openstego.png
Channel 1:
[(98, 99, 1), (108, 109, 1), (155, 154, -1), (182, 183, 1), ...]
[(157, 156, -1), (134, 135, 1), (78, 79, 1), (74, 75, 1), ...]
[(88, 89, 1), (116, 117, 1), (121, 120, -1), (128, 129, 1), ...]
[(131, 130, -1), (111, 110, -1), (96, 97, 1), (99, 98, -1), ...]
[(128, 129, 1), (139, 138, -1), (145, 144, -1), (123, 122, -1), ...]
[(208, 209, 1), (149, 148, -1), (101, 100, -1), (77, 76, -1), ...]
[(104, 105, 1), (134, 135, 1), (128, 129, 1), (131, 130, -1), ...]
[(98, 99, 1), (98, 99, 1), (107, 106, -1), (138, 139, 1), ...]
[(217, 216, -1), (174, 175, 1), (151, 150, -1), (84, 85, 1), ...]
...
We see that pixels are usually modified by one unit. For example, the original value of the first modified pixel is 98, which is modified to 99, a +1 operation. The third is a pixel with value 155 which becomes 154, an operation of -1. The important detail to pay attention to is that the operations are not indiscriminately +1 or -1 (which would indicate that it is LSB matching), but that the odd pixels are always modified with -1 and the even with +1. This tells us that LSB replacement is being used, since it is precisely the effect of replacing the least significant bit of each pixel.
If we run the same command with the OpenPuff images, we get similar results:
./aletheia.py print-diffs peppers3.png peppers3_openpuff.png
Channel 1:
[(147, 146, -1), (177, 176, -1), (177, 176, -1), (169, 168, -1), ...]
[(181, 180, -1), (180, 181, 1), (179, 178, -1), (178, 179, 1), ...]
[(176, 177, 1), (175, 174, -1), (165, 164, -1), (170, 171, 1), ...]
[(184, 185, 1), (159, 158, -1), (144, 145, 1), (186, 187, 1), ...]
[(191, 190, -1), (192, 193, 1), (186, 187, 1), (187, 186, -1), ...]
[(144, 145, 1), (149, 148, -1), (199, 198, -1), (200, 201, 1), ...]
[(201, 200, -1), (198, 199, 1), (201, 200, -1), (200, 201, 1), ...]
[(180, 181, 1), (179, 178, -1), (180, 181, 1), (183, 182, -1), ...]
[(183, 182, -1), (183, 182, -1), (183, 182, -1), (209, 208, -1), ...]
...
Structural steganalysis
Since we know LSB replacement is being used, we can use all the attacks Aletheia implements for this type of steganography. Here we will use two attacks: The SPA attack (Sample Pairs Analysis) and the WS (Weighted Stego) attack, two efficient and precise attacks. In all cases, as a reference, we will first carry out an attack on the cover image and then an attack on the image with the hidden message (stego).
The SPA attack (Sample Pairs Analysis)
Cover images:
$ ./aletheia.py spa monarch.png
No hidden data found
$ ./aletheia.py spa peppers3.png
No hidden data found
Stego images:
$ ./aletheia.py spa monarch_openstego.png
Hiden data found in channel R 0.07493448209001959
Hiden data found in channel G 0.0676341653177243
Hiden data found in channel B 0.05826279404860022
$ ../aletheia.py spa peppers3_openpuff.png
Hidden data found in channel R 0.1464232217001414
Hidden data found in channel G 0.15585640405139609
Hidden data found in channel B 0.11567700466149547
The WS attack (Weighted Stego)
Cover images:
$ ./aletheia.py ws monarch.png
No hidden data found
$ ./aletheia.py ws stego/aletheia/resources/peppers3.png
No hidden data found
Stego images:
$ ./aletheia.py ws monarch_openstego.png
Hiden data found in channel R 0.07295581176434245
Hiden data found in channel G 0.07493768934615823
Hiden data found in channel B 0.06355771697762562
$ ./aletheia.py ws stego/aletheia/resources/peppers3_openpuff.png
Hidden data found in channel R 0.13275428291180907
Hidden data found in channel G 0.13427208873412433
Hidden data found in channel B 0.11806703947840881
Brute force attack on OpenStego
Aletheia implements brute force attacks on different steganography tools. This can be useful if we know, or suspect, that a specific tool has been used and we want to obtain the password and the hidden message.
First, let’s see how to carry out an attack on the well-known tool OpenStego.
We hide a message in a PNG image protected by password:
$ openstego embed -p 123456 -mf secret.txt -cf sample_images/lena.png -sf stego.png
Next, we use Aletheia to find the password and extract the message:
./aletheia.py brute-force-openstego stego.png resources/passwords.txt
Using 16 processes
Completed: 0.0%
Password found: 123456
LSB matching: a simple alternative to LSB replacement
It is curious that steganography tools that use LSB replacement are still being developed, when there are attacks as powerful as those that have been shown. Mainly, taking into account that there is an alternative as simple as the LSB replacement itself that avoids all these attacks. This is the LSB matching.
Instead of substituting those LSBs that do not match the bits of the message that we want to hide, what we have to do is add or subtract one from those values. The effect on LSB is exactly the same, but this way of hiding data does not produce the statistical anomalies that make LSB replacement so detectable.
Returning to the example with which the article was started, if we have the following values in binary:
| R | G | B |
| 10100000 | 00111100 | 00110101 |
| 10000000 | 01101111 | 00101011 |
| 01010100 | 01111101 | 01111101 |
and we want to hide the byte 01000001 corresponding to the letter ‘A’, we can do it by adding or subtracting one randomly, when necessary:
| R | G | B |
| 10100000 | 00111101 (+1) | 00110110 (+1) |
| 10000000 | 01101110 (-1) | 00101010 |
| 01010100 | 01111101 | 01111101 |
As can be seen from the example, the fundamental difference between LSB replacement and LSB matching is that the latter produces carry while the former does not. In fact, LSB replacement never adds one to an odd value and never subtracts one from an even value, producing the anomaly exploited by structural detection methods.
There are currently no comments on this article.
Add a Comment